Lecture 5-1
Statistical Analysis
of Urban Data

Hamish Gibbs

Network Science Institute | Northeastern University

NETS 7983 Computational Urban Science

2025-03-31

Spatial data in CUS

Computational Urban Science is primarily concerned with spatially embedded features of cities.

Some features are explicitly spatial: commuting and infrastructure networks, physical amenity visitation.

Some features are influenced by space: Social, communication, employment / opportunity networks.

• Remember from last week’s practical: higher likelihood of within-state friendships.

Spatial data is unique

The spatial structure of urban data requires special consideration.

Consider Tobler’s first “law” of Geography: “Everything is related to everything else, but near things are more related than distant.”

In CUS, we want reliable, repeatable insights about urban systems. If everything is related to everything else:

• How can we achieve reliable statistical estimates of the relationship between urban variables?

• How can we measure causal relationships in spatially-interconnected systems?

Key takeaway: proximity and adjacency

In Week 2, we discussed the Modifiable Areal Unit Problem (MAUP) and the effect of scale for defining analytical conclusions.

Today, we will use many definitions of proximity and adjacency as we aim to encode the spatial structure of our data into our analysis.

How do we define which things are “near” one another as described in Tobler’s law? Euclidean distance? Geodesic distance? Travel time? Semantic distance?

How do we define adjacency? \(k\) nearest-neighbors? What is \(k\)? What about physical boundaries between physically adjacent features?

Like MAUP, appropriate definitions of spatial structure in your data require your own scientific judgment.

Key takeaway: proximity and adjacency

A tale of two cities: London’s rich and poor in Tower Hamlets

Key takeaway: proximity and adjacency

A tale of two cities: London’s rich and poor in Tower Hamlets

Empirical regularities in spatial data

Is Tobler’s First Law a Law? I prefer “empirical regularities”.

Spatial features have consistent, repeated patterns which should inform how you address statistical and causal inference and other analyses of spatial data.

Some of these regularities are:

• Spatial autocorrelation (a.k.a. “clustering” or spatial heterogenity)

• Spatial nonstationarity (variation of statistical relationships across space)

• Physical constraints on network structure

Spatial autocorrelation

Tobler’s first law revisited: “…near things are more related than distant.”

This is an empirical observation which holds true for a wide range of spatial phenomena.

Spatial autocorrelation permits:

• Prediction / interpolation based on physical proximity.

Spatial autocorrelation hinders:

• Statistical inference (independence assumptions are violated for most spatial data)

Spatial autocorrelation

A funny example: Inverse-distance Weighting (IDW) (1965) beats Google Research’s (2024) elevation predictions:

General Geospatial Inference with a Population Dynamics Foundation Model

Measuring spatial autocorrelation

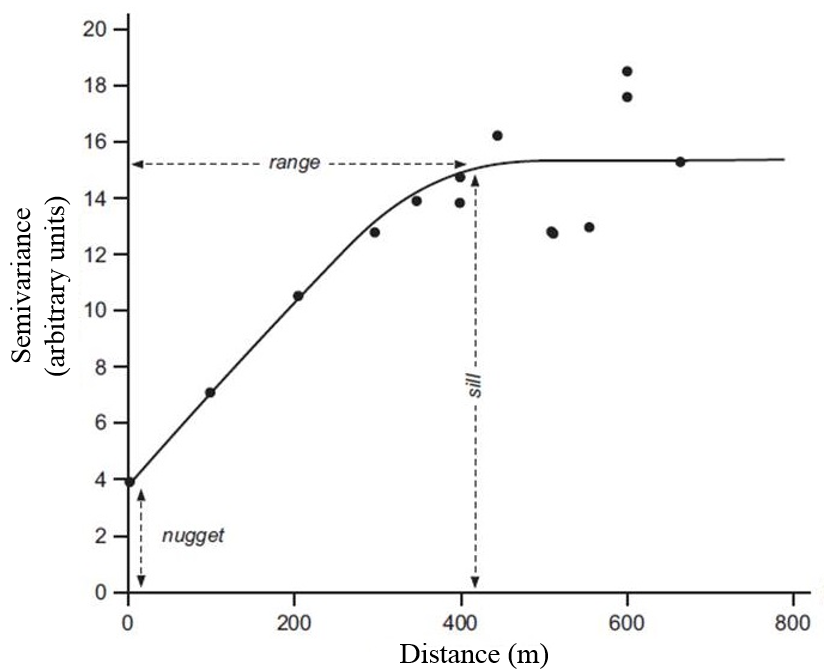
Spatial variogram: how much do two observations vary by distance?

Useful for assessing degree of spatial autocorrelation of continuous spatial variables.

Variogram and spatial autocorrelation

Measuring spatial autocorrelation

Moran’s I

• Global measure of spatial clustering typically ranging from -1 (perfect dispersion) to 1 (perfect clustering).
• Measures how much a value at one location is correlated with values at nearby locations.

[An Introduction to] Hotspot Analysis Using ArcGIS

Measuring spatial autocorrelation

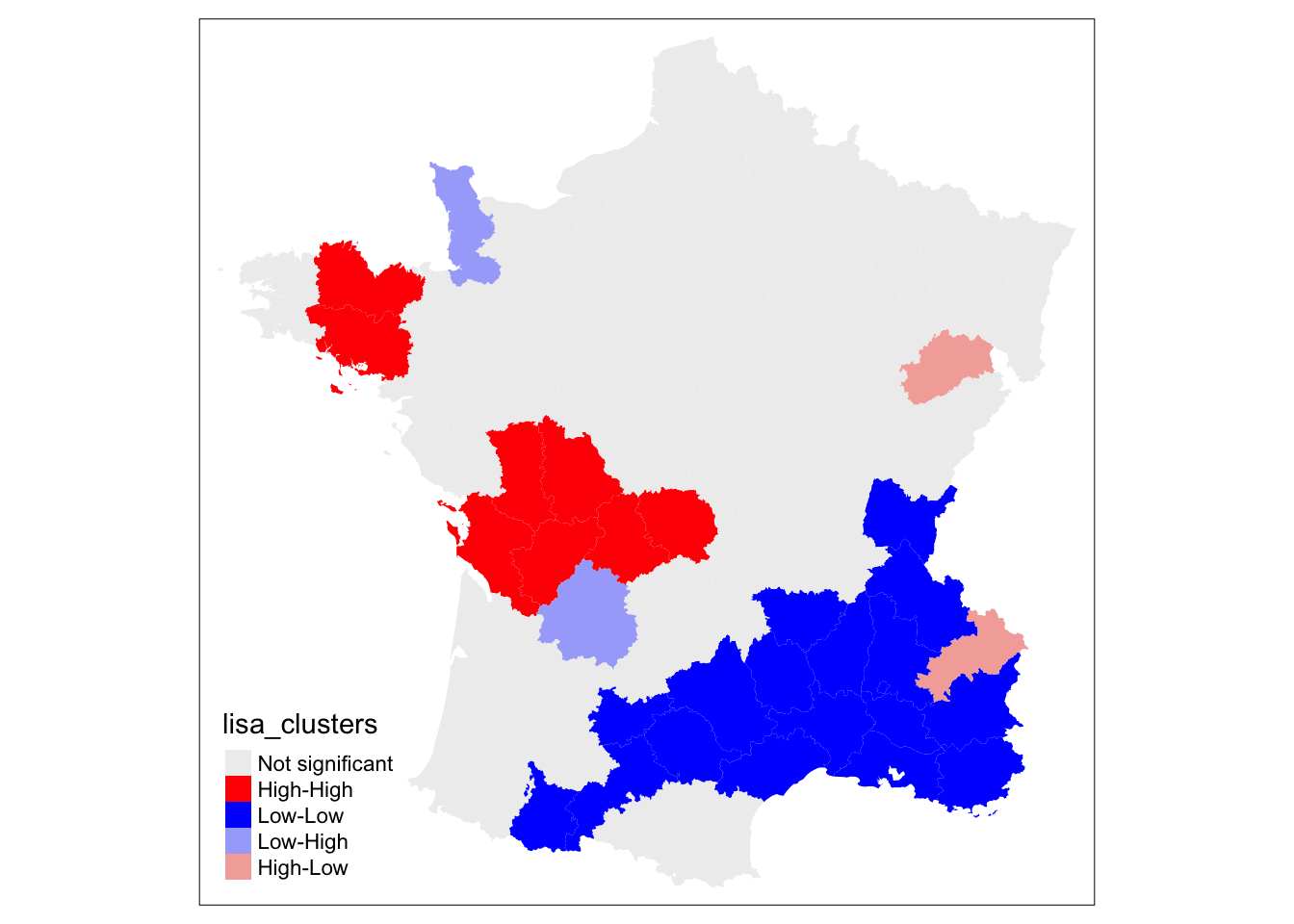
Local Indicators of Spatial Association (LISA)

• Local version of Moran’s I, assigned to each area and compared to an area’s neighbors.
• LISA results are expressed as the the value of a spatial variable relative to neighbors and the global mean:
  • “High-High” or “Low-Low” (High / Low local value with High / Low values of neighbors - i.e. spatial clusters)
  • “Low-High”, “High-Low” (High / Low local value with Low / High values of neighbors - i.e. spatial outliers)

Hands-On Spatial Data Science with R: Chapter 12 Local Spatial Autocorrelation 1

Spatial nonstationarity

Another feature of spatial data: statistical relationships can vary across space

There are multiple techiques to address spatial autocorrelation and nonstationarity:

• Geographically weighted regression:

  • Estimates local regression coefficients, giving greater weight to nearby observations

• Fixed effects models:

  • We used one last week!

  • Used to handle unobserved location-specific variation that impacts dependent variables. Only allows interpretation of within-unit effects.

More on GWR and spatially-aware statistical inference next week!

Warning: Edge / Boundary Effects

Most geostatistical analysis happens within a constrained spatial boundary

For proximity- or adjacency-based statistical methods (like GWR):

• Boundary locations can show spurious statistical relationships because of a lack of neighbors in the adjacency matrices used to parameterize models

An evaluation of edge effects in nutritional accessibility and availability measures: a simulation study

Spatial clustering

Spatial clustering techniques account for spatial proximity when defining clusters.

Supports varying cluster density (producing varying size clusters).

Spatial clustering is useful for: dimensionality reduction of spatial features and for detecting spatial outliers.

In practical 5-1: note the difference between K-means clusters and geographically contiguous SKATER clusters (SKATER accounts for spatial proximity).

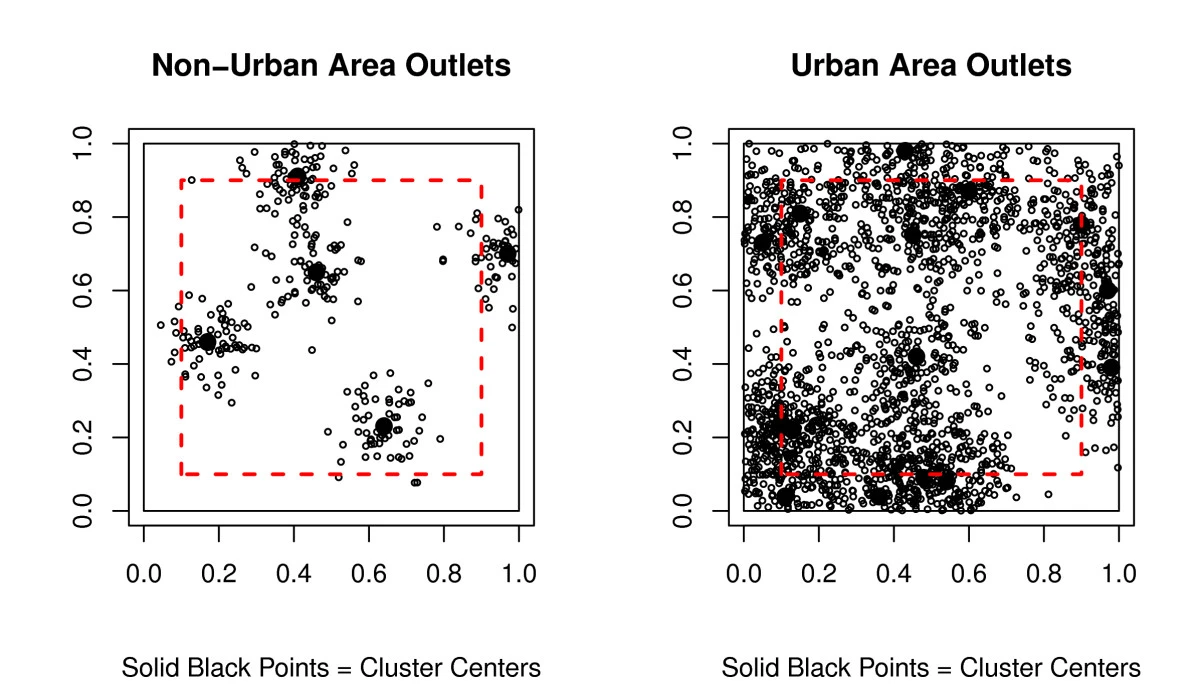
DBSCAN - Density Based Spatial Clustering of Applications with Noise

Spatial clustering algoritms

Most common spatial clustering algorithms:

• DBSCAN
  • Defined by two variables:
  • \(minPts\): Minimum density of points defining core points (cluster centers).
  • \(\varepsilon\) Maximum distance required to define border points connected to core points with neighbors \(< minPts\).
  • Outliers are \(> \varepsilon\) distance from core points.

For \(minPts = 4\), \(\varepsilon\) indicated by circle radius. Red: core points, Yellow: border points, Blue: outlier.

Spatial clustering algoritms

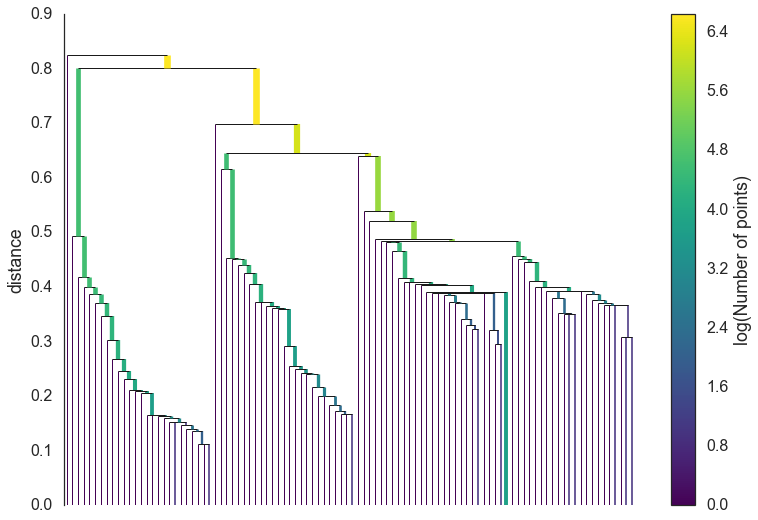
• HDBSCAN
• Replaces a single \(\varepsilon\) for a range of distance values defined by a minimum spanning tree of mutual reachability between each data point and its \(minPts\) nearest neighbors.

hdbscan Python Package: How HDBSCAN Works

Spatially embedded networks

Spatial networks have unique characteristics driven by their spatial embeddedness.

• Edge formation is driven by physical cost

• Therefore, spatial networks typically have fewer long-range ties compared to non-spatial networks

• Spatial networks are typically described by weighted, directed networks

  • Edge weights can represent many forms of distance: euclidean, routing, time, attractiveness

• Spatial networks tend to have hierarchical structure

  • Hierarchical structure is seen in the presence of highly central “hubs”

Hierarchical structure in spatial networks

Hub structures, modularity in spatial networks results from the benefits of co-location and hierarchical organization.

Source: The Origins of Scaling in Cities [1].

References

[1]

L. M. A. Bettencourt, “The Origins of Scaling in Cities,” Science, vol. 340, no. 6139, pp. 1438–1441, Jun. 2013, doi: 10.1126/science.1235823.