library(tidyverse)
library(arrow) # for efficient dataframes
library(DT) # for interactive tables
library(knitr) # for tables
library(ggthemes) # for ggplot themes
library(sf) # for spatial data
library(tigris) # for US geospatial data
library(tidycensus) # for US census data
library(stargazer) # for tables
library(leaflet) # for interactive maps
library(igraph) # for network analysis
library(ggraph) # for network visualization
set.seed(12345) # for reproducibility
options(tigris_use_cache = TRUE) # use cache for tigris
theme_set(theme_hc() + theme(axis.title.y = element_text(angle = 90))) Lab 11-1 - Epidemics using ABMs
Objectives
In this lab, we will use Agent-Based Models (ABMs) to understand the evolution of epidemics in urban areas. We will use a simple agent model to model people’s mobility in urban areas leading to contacts between them and simulate a simple SIR model over that network of contacts. In particular, we will
- Use individual mobility data to model the mobility of agents in the city and the contacts between them.
- A simple SIR model will be used to simulate the spread of diseases in the city.
- Analyze the dynamics of the spread of diseases in the city and the impact of the different places in the propagation of the epidemic.
- Simulate different non-pharmaceutical interventions to control the spread of diseases in the city.
Load some libraries and settings we will use
Agent-based model
To simulate the spread of diseases in cities, we define a simple agent-based model. In this model:
- Agents move around the city visiting different POIs.
- As a result of that mobility, agents can get in contact / exposure with other agents in particular POIs.
- Agents can infect each other when they encounter.
- We will discard home infection, although it can be included in the model.
Mobility
Each agent has a particular type of mobility, visiting different POIs in the city during the day. Agents’ mobility can be modeled in two different ways:
- The mobility of agents can be modeled using a simple decision-making model, for example, using the Exploration and Preferential Return model using gravity models to visit new places.
- Mobility of agents can also be data-driven modeled:
- We can use actual mobility data from aggregated flows (Advan) and generate random walks using those flows,
- Agent mobility can be taken directly from individual mobility data (Cuebiq).
Epidemic model
We will use a simple SIR model to simulate the spread of diseases in the city. In this model, agents can be in three states:
- Susceptible (S): agents that can be infected.
- Infected (I): agents that are infected and can infect others.
- Recovered (R): recovered agents that cannot be infected again.
The dynamics of the model are simple:
\[ \begin{aligned} S & \xrightarrow{\beta} I \\ I & \xrightarrow{\gamma} R \end{aligned} \]
where:
- Susceptible agents \(S\) can be infected when they encounter an infected agent \(I\) in a POI with probability \(\beta\). We will assume that the probability is constant across all POIs.
- Infected agents recover at rate \(\gamma\). For simplicity, we will assume that agents recover after a fixed number of days (\(1/\gamma\)). After recovery, agents get immunized and cannot be infected again.
Data-drive Agent-Based model
Since we have the individual mobility data for 10k users in the Boston MSA, instead of modeling the mobility of the agents, we will use a data-driven approach to simulate their mobility.
visits <- read_csv("/data/CUS/mob10kusers.csv")On the other hand, we will simulate the epidemics using a simple SIR model. We will only consider that this is possible if users spend more than 5 minutes in a given POI so there is enough time for epidemic contact.
visits <- visits |>
filter(DWELL_TIME_MINUTES >= 5 & DWELL_TIME_MINUTES <= 60*4)ABM simulation of epidemics
To simulate the epidemics, we need to identify when users get in contact. For simplicity, we will assume that if two users spent some time in a given POI on the same day, there is a contact between them. This condition can be strengthened by requiring that users spend time in the same POI simultaneously.
Here is the list of days:
days <- unique(as.Date(visits$TIME)) |> sort()For example, this is the table with the number of contacts on the first day
vv <- visits |> filter(as.Date(TIME) == days[1])
contacts <- vv |>
inner_join(vv, by = c("VISIT_CBG" = "VISIT_CBG", "ACTIVITY" = "ACTIVITY"),
relationship = "many-to-many") |>
filter(USER.x != USER.y) |>
dplyr::select(USER.x, USER.y, VISIT_CBG, ACTIVITY)Note that, as we did in previous labs, we are considering the pair VISIT_CBG and ACTIVITY to identify the POI. This is a simplification, but it is enough for our purposes.
The table contacts contains the daily contact network in the city of those 10k agents.
contact_network <- graph_from_data_frame(contacts, directed = FALSE)Contacts are very heterogeneous, with some users having many contacts and most of them having few contacts.
contact_network |> degree() |> enframe() |>
ggplot(aes(value)) +
geom_density(fill="lightgray",alpha=0.5) +
scale_x_log10() +
labs(x="#Contacts", y="Density")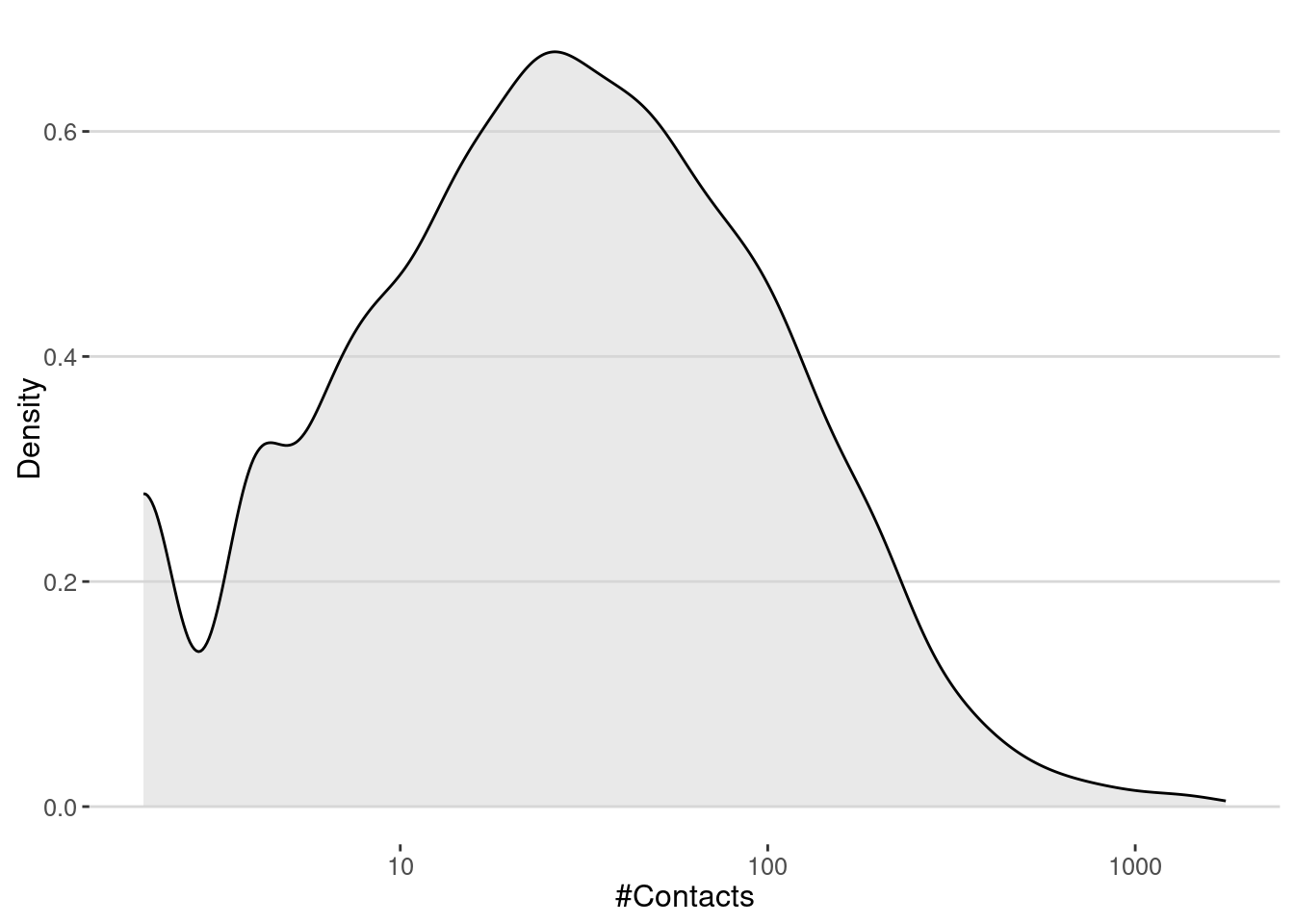 
The number of contacts is very important to understand the spread of diseases in the city. In particular, the famous \(R_0\) is proportional to the average number of contacts in the network. In our case, we get that the average number of contacts is
cat("<k> = ",mean(degree(contact_network)),"\n")<k> = 60.35777 Thus, if we make the simple assumption that the number of secondary cases on average is \(R_0 = \langle k \rangle \beta\), we can estimate that the critical transmission probability of a pandemic is
cat("Critical transmission probability, beta_c =",1/mean(degree(contact_network)),"\n")Critical transmission probability, beta_c = 0.01656787 Simulate the spread of diseases
To simulate the spread we will use the following algorithm:
- First we simulate the transmission of the disease from \(I \to S\). To do that we get all the contacts at day \(t\), get only the ones between \(S\) and \(I\) groups and sample them with probability \(\beta\) to get the infection events. If
old_infectedandold_susceptiblethe sets of infected and susceptible agents at day \(t\), we can get the transmission events as follows:
beta = 0.03
transmission <- contacts |> sample_n(beta*nrow(contacts)) |>
filter((USER.x %in% old_infected & USER.y %in% old_susceptible) |
(USER.y %in% old_infected & USER.x %in% old_susceptible)
)- The new infected agents are
new_infected <- unique(c(transmission$USER.x, transmission$USER.y))
new_infected <- new_infected[!new_infected %in% old_infected]After that, we can check how long a node has been infected and if it is time to recover it to implement the \(I \to R\) transition.
We repeat this process for another day until there is no longer any agent in the infected state.
Let’s put all together in a function that simulates the spread of diseases in the city from a table of visits. This function returns two tables:
table_usersincludes the final information for all agents: their final status and the time of infection.transmission_tablehas all the transmission \(S \to I\) events, including the origin of infection, the time, and the place of the infection.
gen_epidemic <- function(visits, ini.infected = 10,
beta = 0.03,r.days=7,
cats.excluded = ""){
#exclude visits to certain categories
visits <- visits |> filter(! ACTIVITY %in% cats.excluded) |>
mutate(TIME = as.Date(TIME))
#get the unique days
days <- unique(visits$TIME) |> sort()
#initialize the status of each user on the first day
#all users are susceptible and ini.infected of them are infected
table_users <- tibble(
USER = unique(visits$USER), STATUS = "S", TINF = NA
)
infected <- sample(table_users$USER, ini.infected)
table_users <- table_users |>
mutate(STATUS = if_else(USER %in% infected, "I", STATUS),
TINF = if_else(USER %in% infected, as.Date(days[1]), TINF))
transmission_table <- data.frame()
new_infected <- infected
#loop over the rest of the days
for(i in 2:length(days)){
#select the visits today
vv <- visits |> filter(TIME == days[i])
#this is the group in the infected "I" status and the susceptible "S" status
old_infected <- table_users$USER[table_users$STATUS == "I"]
old_susceptible <- table_users$USER[table_users$STATUS == "S"]
#### S -> I ####
#get the contacts between users in the same CBG and ACTIVITY pairs
contacts <- vv |>
inner_join(vv, by = c("VISIT_CBG" = "VISIT_CBG", "ACTIVITY" = "ACTIVITY"),
relationship = "many-to-many") |>
filter(USER.x != USER.y) |>
dplyr::select(USER.x, USER.y, VISIT_CBG, ACTIVITY)
#Those contacts transmit the disease with probability beta
transmission <- contacts |> sample_n(beta*nrow(contacts)) |>
filter((USER.x %in% old_infected & USER.y %in% old_susceptible) |
(USER.y %in% old_infected & USER.x %in% old_susceptible)) |>
mutate(TIME = days[i])
#get the new infected
new_infected <- unique(c(transmission$USER.x, transmission$USER.y))
new_infected <- new_infected[!new_infected %in% old_infected]
#order the transnmission event and keep only the first transmission
#between users
transmission <- transmission |>
mutate(user_i = if_else(USER.x %in% old_infected, USER.x, USER.y),
user_s = if_else(USER.x %in% old_infected, USER.y, USER.x)) |>
arrange(user_s) |> distinct(user_s,.keep_all = TRUE) |>
dplyr::select(user_i,user_s,TIME,VISIT_CBG,ACTIVITY)
#add the new transmission events to the table
transmission_table <- rbind(transmission_table,transmission)
#update the status of the users for the infections
if(length(new_infected) > 0){
table_users <- table_users |>
mutate(STATUS = if_else(USER %in% new_infected, "I", STATUS),
TINF = if_else(USER %in% new_infected, as.Date(days[i]), TINF))
}
#### I -> R
# update the status of the users for the recoveries
table_users <- table_users |>
mutate(STATUS =
if_else(STATUS == "I" & TINF + r.days <= days[i], "R", STATUS))
}
return(list(transmission_table=transmission_table,
table_users=table_users))
}Epidemic spreading without interventions
Let’s simulate the spread of diseases in the city without any intervention. We will use the function gen_epidemic to simulate the spread of diseases in the city.
epidemic_no_NPI <-
gen_epidemic(visits,
ini.infected = 10,
beta = 0.03,
cats.excluded = "")Here is the number of cases by day
cases_epidemic_no_NPI <-
epidemic_no_NPI$table_users |>
filter(!is.na(TINF)) |>
count(TINF)
ggplot(cases_epidemic_no_NPI,aes(x=TINF,y=n)) +
geom_line() +
labs(x="Date",y="Number of cases")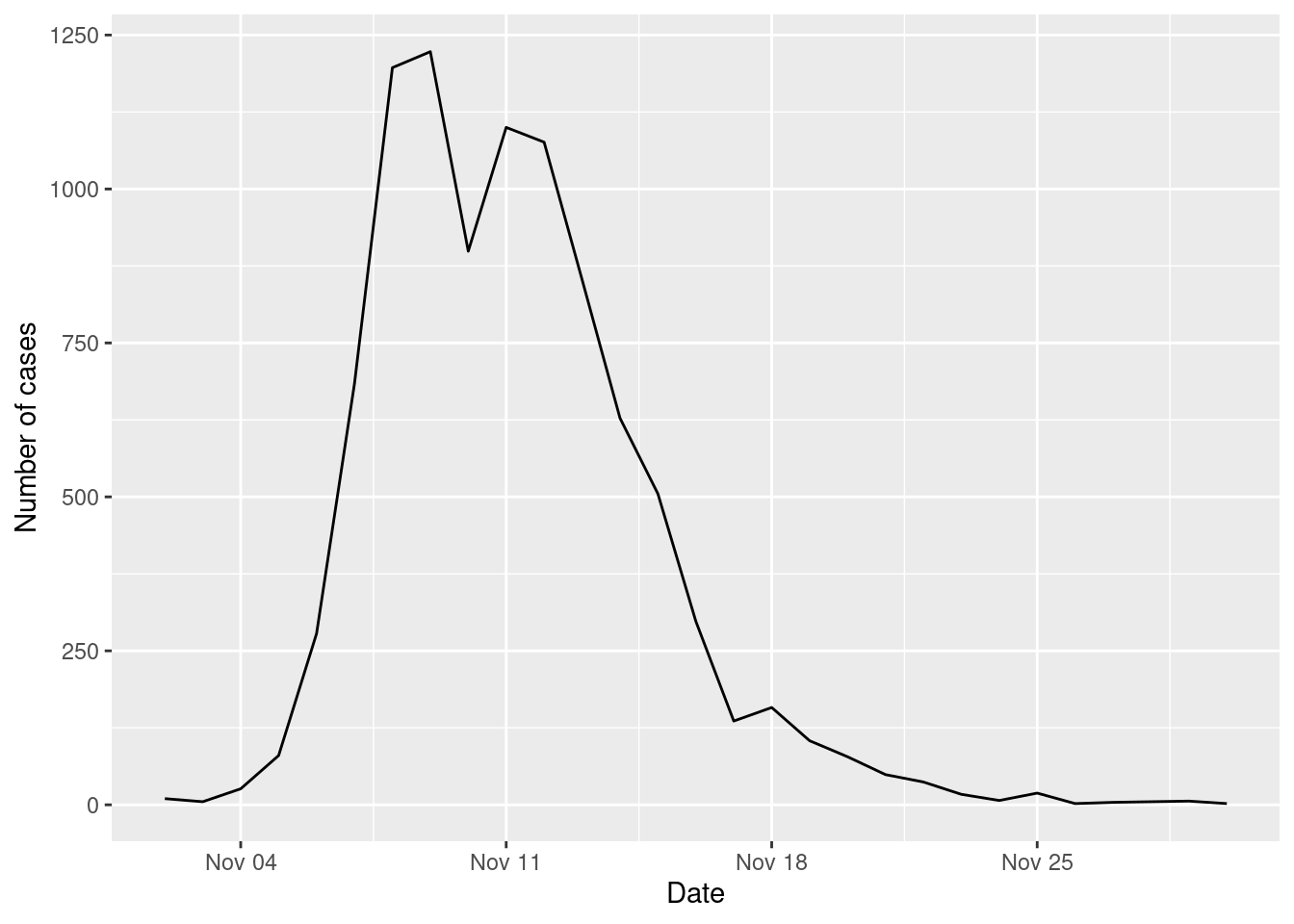
Impact of type of places on the epidemic spreading
We can also investigate the places where most transmissions took place
ggplot(epidemic_no_NPI$transmission_table) +
geom_bar(aes(x=TIME,y=after_stat(count),fill=ACTIVITY),
stat="count",position="stack") +
scale_fill_tableau(palette = "Tableau 20")+
labs(x="Date",y="Number of infections")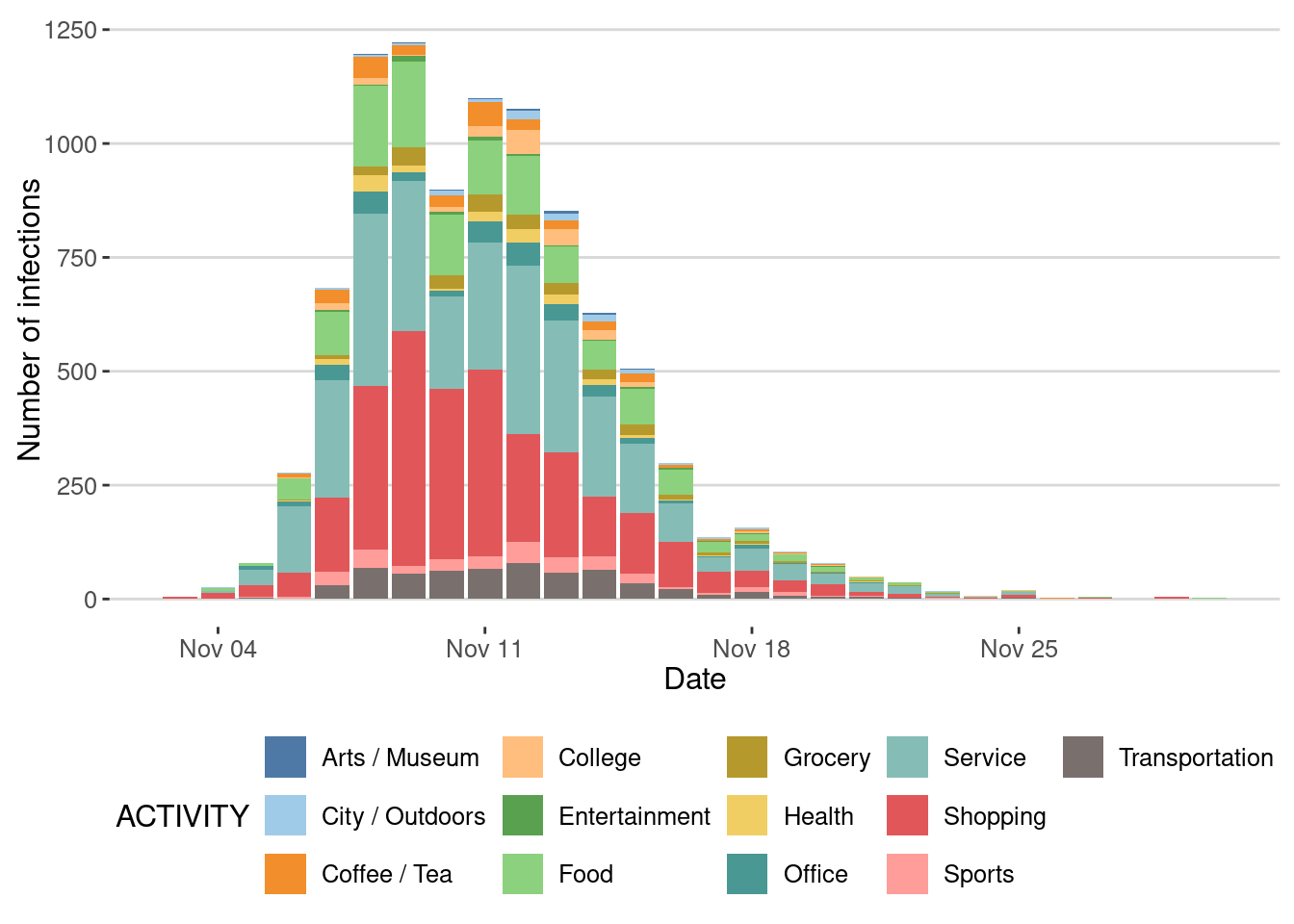
Or by fraction
ggplot(epidemic_no_NPI$transmission_table) +
geom_bar(aes(x=TIME,y=after_stat(count),fill=ACTIVITY),
stat="count",position="fill") +
scale_fill_tableau(palette = "Tableau 20")+
labs(x = "Date",y ="Fraction of infections")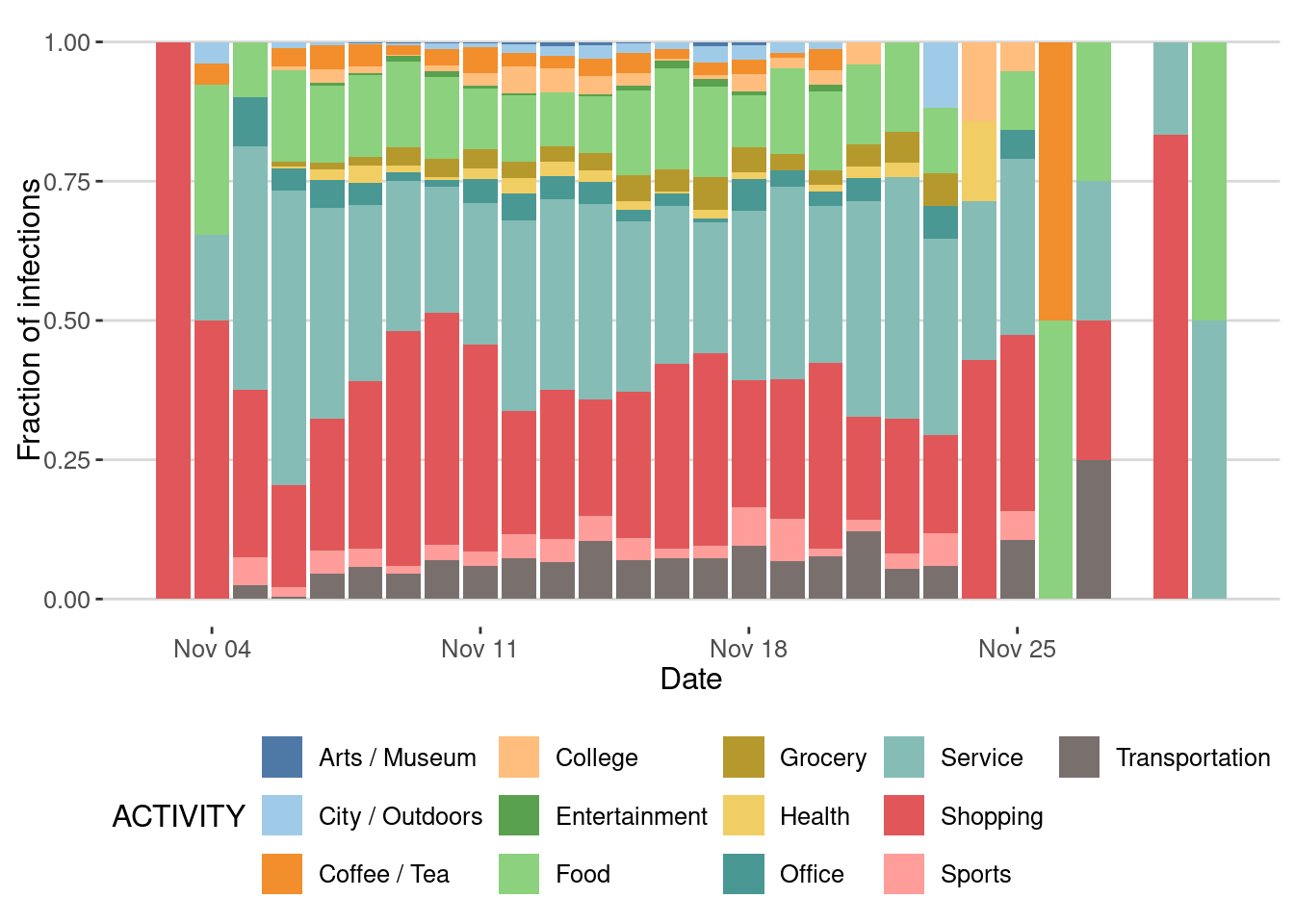
Super-spreading events
One of the key signatures of different epidemic processes is the presence of super-spreading events [1]. These events are characterized by a single individual infecting a large number of other individuals.
Let’s see those events as a cascade of infections:
g <- graph_from_data_frame(epidemic_no_NPI$transmission_table, directed=T)
ggraph(g, layout = 'tree') +
geom_edge_diagonal(alpha=0.1) +
geom_node_point(aes(size=degree(g,mode="out")),
col=rgb(0.6,0.2,0,0.5))+
scale_size(name="Secondary Cases") +
theme_void()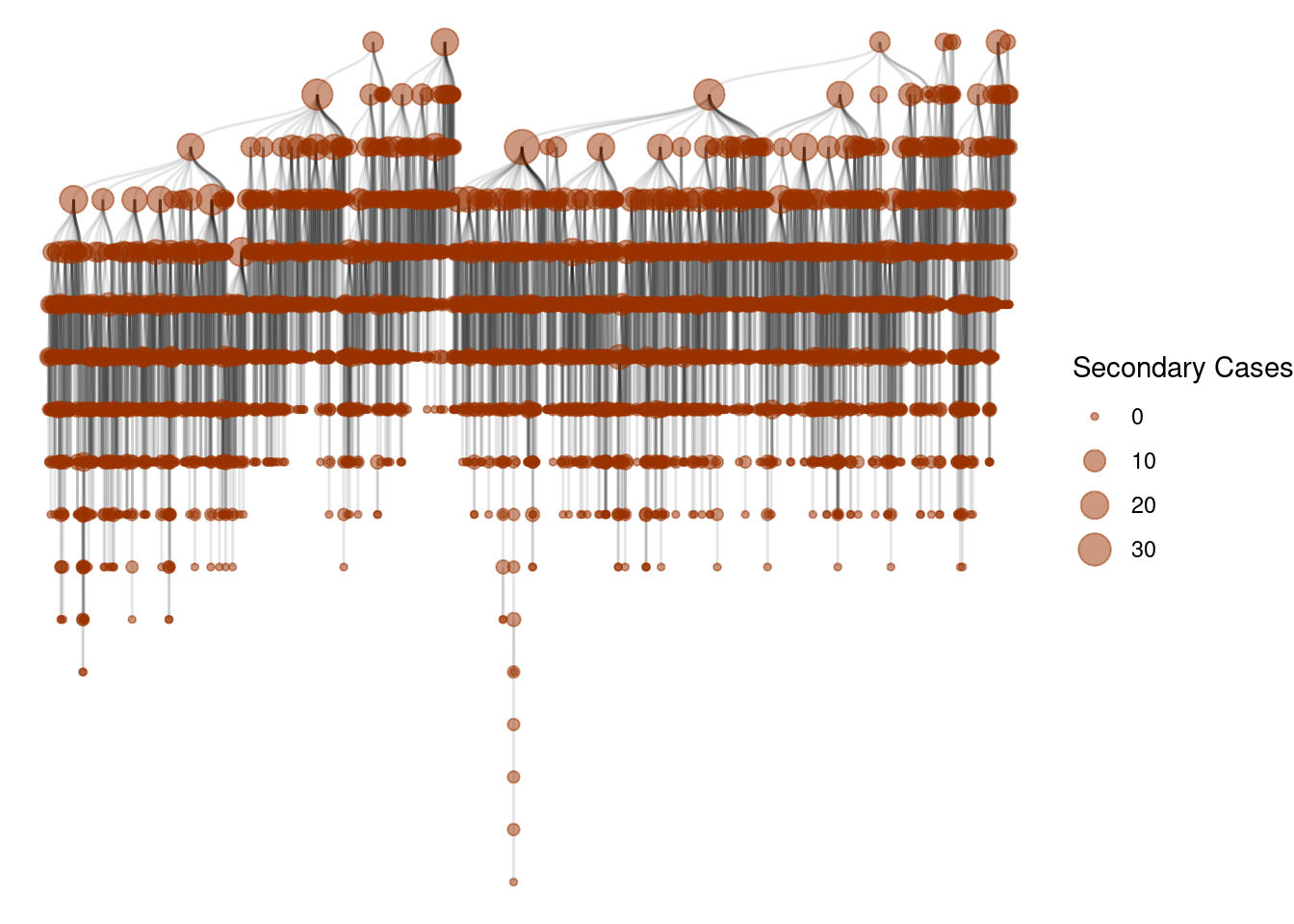
And this is the distribution
secondary_cases <- degree(g,mode="out")
ggplot(data.frame(sc=secondary_cases),aes(x=sc)) +
geom_density(color="black") +
scale_x_log10() + scale_y_log10() +
labs(x="Number of secondary cases",y="Density")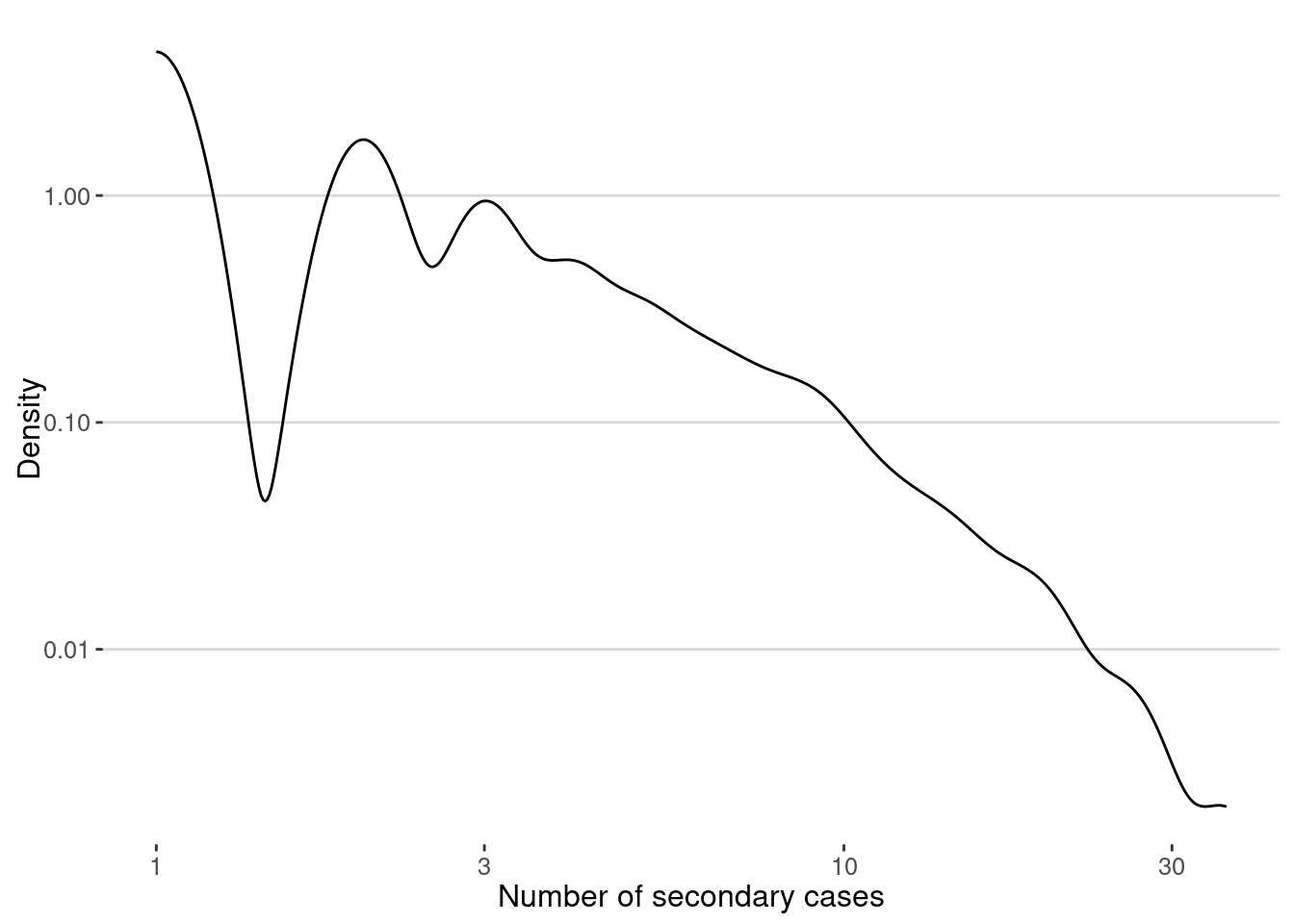
The average of secondary cases is the famous \(R_0\) of the epidemic. In our case we get:
cat("R0 = ",mean(secondary_cases),"\n")R0 = 0.999156 Note that, since the outbreak has stoped we get \(R_0 < 1\).
However, the number of secondary cases is very heterogeneous, with some users infecting many others, creating those super-spreading events. One way to measure the relevance of superspreading events is to calculate dispersion parameter, \(\kappa\), assuming that the number of secondary cases is distributed like a Negative Binomial [1].
This parameter can be estimated using the moments of the distribution. If the number of secondary cases \(r_i\) generated by each infected individual \(i\) then \[ \kappa = \frac{ \overline{r_i}^2}{Var(r_i) - \overline{r_i}} \] Here is the function to calculate it:
dispersion <- function(sec_cases){
mean_x <- mean(sec_cases)
var_x <- var(sec_cases)
mean_x^2 /(var_x-mean_x)
}In our case we get
cat("Dispersion parameter, k =",dispersion(secondary_cases),"\n")Dispersion parameter, k = 0.3911538 More formally, we can fit the distribution to a Negative Binomial and get the dispersion parameter directly
library(MASS)
fit <- fitdistr(secondary_cases, "Negative Binomial")
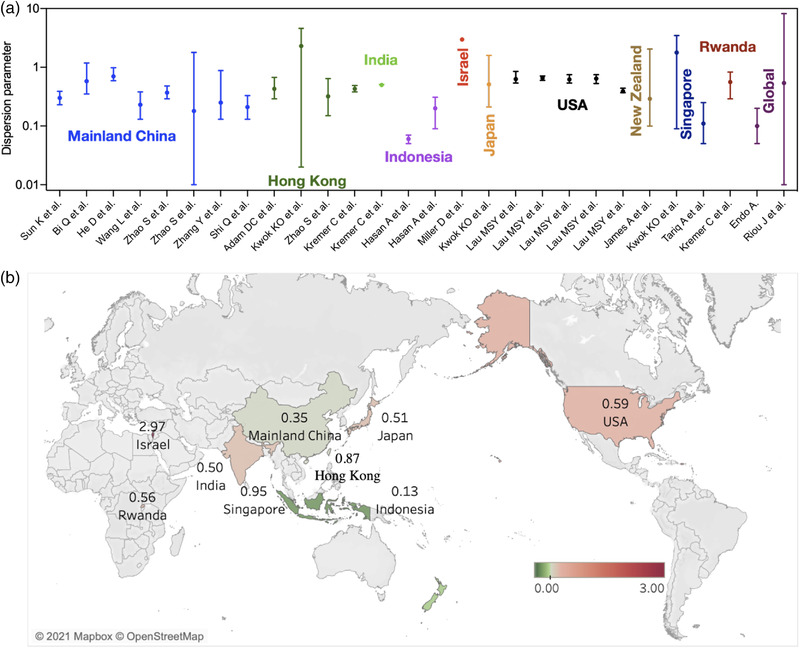
cat("Dispersion parameter, k = ",fit$estimate["size"],"\n")Dispersion parameter, k = 0.5573663 You can compare it to different measures of dispersion coefficient with epidemics, like COVID-19:
Your turn
In a recent paper [3], Aleta and collaborators simulate different NPI strategies to control the spread of diseases in cities. Use our ABM to implement the following strategies:
- Non-essential business closure: close all non-essential businesses, like restaurants, museums, offices, etc.
- Social distancing: reduce the number of contacts between agents by 50%.
- Quarantine: isolate the infected agents for 14 days.
Reproduce the results above for each of the strategies and compare the impact of each of them on the spread of diseases in the city.
Epidemic spreading with non-essential business closure
For example, this the simulation of the spread of diseases with the non-essential business closure strategy:
epidemic_NPI <-
gen_epidemic(visits,
ini.infected = 10,
beta = 0.03,
cats.excluded = c("Food","Office",
"Arts / Museum",
"Entertainment",
"Sports",
"Shopping"))and here is the number of cases
cases_epidemic_essential <- epidemic_NPI$table_users |>
filter(!is.na(TINF)) |>
count(TINF)
ggplot(cases_epidemic_essential,aes(x=TINF,y=n)) +
geom_line() +
labs(x="Date",y="Number of cases")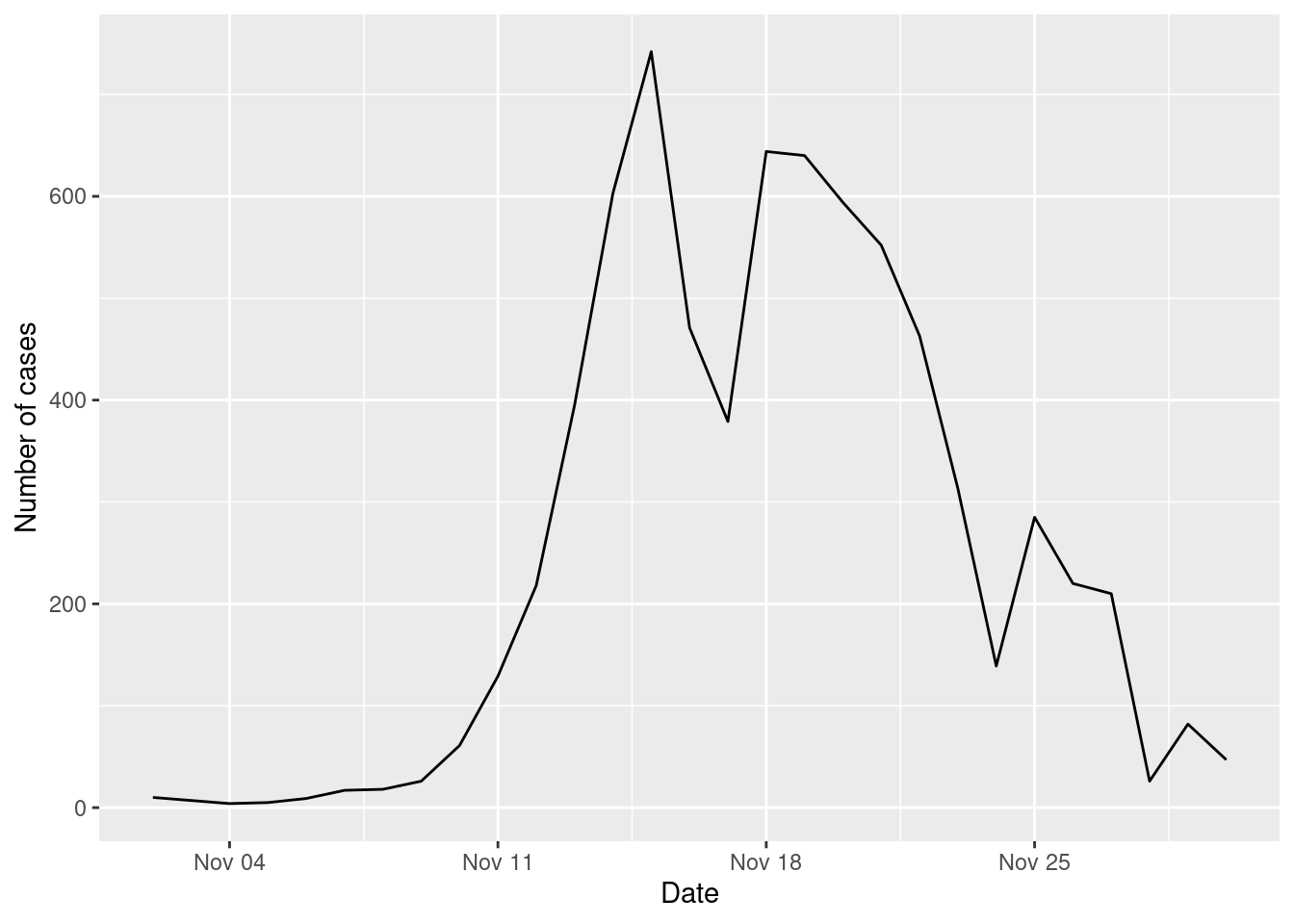
Compare the number of cases with and without the NPI
cases_epidemic_no_NPI |>
mutate(NPI = "No NPI") |>
bind_rows(cases_epidemic_essential |>
mutate(NPI = "Essential closure")) |>
ggplot(aes(x=TINF,y=n,color=NPI)) +
geom_line() +
labs(x="Date",y="Number of cases")
Conclusions
Using ABMs we can simulate the spread of diseases in cities and understand the impact of different interventions on the spread of diseases. In particular, we can understand the importance of super-spreading events and the impact of different places on the spread of diseases.
Agents’ mobility can be defined by simple individual models, like EPR, but also we can use data-driven models to simulate the mobility of agents in the city.
ABMs can help us understand the emergence of epidemic patterns from micro-decisions of agents and the impact of different interventions on the spread of diseases in cities.
Further reading
The Idea of Agent-Based Modeling by Gilbert, in the SAGE Research Methods Book on Agent-Based Modeling [4]
Agent-Based Modeling and the City: a gallery of applications by Crooks et al [5]
Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19 by Aleta et al [3]
References
[1]
J. O. Lloyd-Smith, S. J. Schreiber, P. E. Kopp, and W. M. Getz, “Superspreading and the effect of individual variation on disease emergence,” Nature, vol. 438, no. 7066, pp. 355–359, Nov. 2005, doi: 10.1038/nature04153.
[2]
Z. Du et al., “Systematic review and meta‐analyses of superspreading of SARS‐CoV‐2 infections,” Transboundary and Emerging Diseases, p. 10.1111/tbed.14655, Jul. 2022, doi: 10.1111/tbed.14655.
[3]
A. Aleta et al., “Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19,” Nature Human Behaviour, vol. 4, no. 9, pp. 964–971, Sep. 2020, doi: 10.1038/s41562-020-0931-9.
[4]
N. Gilbert, “The Idea of Agent-Based Modeling,” in Agent-Based Models, SAGE Publications, Inc., 2008, pp. 2–21. doi: 10.4135/9781412983259.
[5]
A. Crooks, A. Heppenstall, N. Malleson, and E. Manley, “Agent-Based Modeling and the City: A Gallery of Applications,” in Urban Informatics, W. Shi, M. F. Goodchild, M. Batty, M.-P. Kwan, and A. Zhang, Eds., Singapore: Springer, 2021, pp. 885–910. doi: 10.1007/978-981-15-8983-6_46.